Blackjack Perfect play

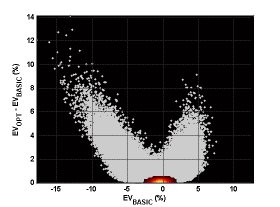What is the overall per-round expected return for these two “endpoint” strategies? The basic strategy player’s expected return is about -0.4239% (note that this value is less than the “full-shoe” expected return quoted in Part 1 due to the cut card effect), while perfect play yields an expected return of only -0.2333%. In other words, even equipped with a laptop at the table, the house still has an advantage! This is not as surprising as it sounds; since we are focusing on playing efficiency, we are assuming flat betting. This merely emphasizes the point that, in shoe games, accurate betting strategy is more important than varying playing strategy.

The figure above essentially shows the “distance” between a basic strategy player and a perfect player. The performance of any actual card counting system, no matter how simple or complex, will lie somewhere in between these two extremes. If we define the playing efficiency of basic strategy to be zero, and the playing efficiency of perfect play to be one, then the efficiency of any other strategy is calculated using its per-round expected return according to

It now remains only to compute this expected return for some actual card counting strategies of interest, and evaluate their corresponding efficiencies.

(A word of caution: before anyone runs off quoting this as “the” formula for playing efficiency, note that these particular constants depend on all of the rule variations, number of decks, and penetration assumed at the outset of this discussion.)

True count indices

The latest additions to my blackjack analysis software allow exact evaluation of indexed playing strategies that vary based on the true count. For example, the most common refinement of basic playing strategy is to hit hard 16 against a dealer ten… unless the true count is zero or greater, in which case you should stand. A more complex example is soft 18 vs. dealer 2. Basic strategy in this situation is to stand, but a more complex index strategy is to hit if the true count is less than -17, stand if it’s less than 1 (but at least -17), otherwise double down.

More generally, we can specify an arbitrarily complex indexed playing strategy as a list of “exceptions” to total-dependent basic strategy. Each exception is identified by a tuple , where

For each of these situations, the indexed playing strategy is given by a partition of the real line into half-open intervals of possible true counts, where each interval corresponds to a particular playing decision, encoded as 1=stand, 2=hit, 3=double down, 4=split, or 5=surrender.

For example, following are the so-called “Illustrious 18” index plays using the Hi-Lo true count. Compare this machine-readable format with the original list generated by Cacarulo at bjmath.com. Note how the playing decisions are interleaved with the true count indices indicating the endpoints of the corresponding intervals, with +1000 acting as “positive infinity.”

• Blackjack team play
• Blackjack table Top
• Black Jack Picture