Blackjack number of decks

Note that the number of decks are indicated on a logarithmic scale, to emphasize the asymptotic behavior of expected return as the number of decks grows large. The question is, why does the player’s expected return increase in games with fewer decks?
“All things being equal, using fewer decks decreases the house edge. This mainly reflects an increased likelihood of player blackjack, since if the players draws a ten on their first card, the subsequent probability of drawing an ace is higher with fewer decks. It also reflects a decreased likelihood of blackjack-blackjack push in a game with fewer decks.”
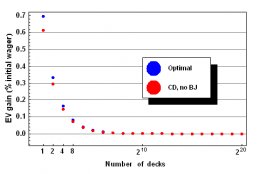
This is a real (and easily calculated) effect, but only a minor secondary one. As we did last week, we can show this by considering a modified game, where the bonuses and penalties associated with blackjacks are removed, and showing that the trend in expected value vs. number of decks still remains. The following plot shows this trend with the points in red, with the points in blue corresponding to the normal game as in Figure 1.
As you can see, the absolute expected return in a “blackjack-less” game is miserable, but that’s not the point. The point is that the trend remains; even with no blackjacks, fewer decks are still better for the player. To see this more clearly (here and in what follows), instead of plotting absolute expected values, let’s normalize the data relative to an “infinite shoe, ” and plot the gain in expected value for a particular number of decks, compared with the expected value for an infinite number of decks (assuming the same rules and playing strategy).
At this point last week, I speculated that the main reason that fewer decks are better is the greater opportunity to vary “composition-dependent” playing strategy, where decisions to stand, hit, etc., may depend not only on the player’s hand total, but on how that total is composed (e.g., is a hard 16 made up of 10-6, or 10-3-3, or 8-4-4, etc.?). With a sufficiently large number of decks, strategy is effectively just “total-dependent, ” since the composition of the hand has a negligible effect on the probability distribution of card ranks remaining in the shoe. (This sufficiently large number of decks turns out to be 125.) But with fewer decks, each individual card dealt from the shoe provides more information to the player, the result being that the player’s strategy is “more composition-dependent” in games with fewer decks.
We can test this theory in a similar fashion, by preventing the playing strategy from varying with number of decks, and seeing if the trend disappears. To do this, we fix the player’s strategy to be the same (total-dependent) optimal strategy for the game with an infinite number of decks… no matter how many decks we are actually playing with. That is, we no longer “know” whether we are playing with fewer decks. The following plot shows the resulting behavior of gain in expected return vs. number of decks.
More:
- If you are not interested in mobile casino , then you have already missed a lot.
Crazy Eights is a shedding-type card game for two to seven players. The object of the game is to be the first to get rid of all the player's cards to a discard pile. The game is considered a pre-extension of Switch and Mau Mau, much favoured in schools during the 1970s.
A standard 52-card deck is used when there are fewer than six players. When...